Die Laplace-funksie is een van die bekendste nie-elementêre funksies wat in wiskunde, in die teorie van differensiaalvergelykings, in statistiek en in waarskynlikheidsleer gebruik word. Om probleme daarmee op te los, verg aansienlike voorbereiding. Kom ons kyk hoe u Excel-gereedskap kan gebruik om hierdie aanwyser te bereken.
Laplace-funksie
Die Laplace-funksie het wye en teoretiese toepassings. Dit word byvoorbeeld gereeld gebruik om differensiaalvergelykings op te los. Hierdie term het 'n ander ekwivalente naam - die waarskynlikheidsintegraal. In sommige gevalle is die basis vir die oplossing die konstruksie van 'n waardetabel.
Operateur NORM.ST.RASP
In Excel word hierdie probleem met behulp van die operateur opgelos NORM.ST.RASP. Die naam is 'n afkorting van die term "normale standaardverspreiding". Aangesien die belangrikste taak is om terug te keer na die geselekteerde sel, is die normale normale integrale verspreiding. Hierdie operateur behoort tot die statistiese kategorie van standaard Excel-funksies.
In Excel 2007 en in vroeëre weergawes van die program, is hierdie verklaring genoem NORMSDIST. Dit word gelaat vir versoenbaarheidsdoeleindes in moderne weergawes van toepassings. Maar tog beveel hulle die gebruik van 'n meer gevorderde analoog aan - NORM.ST.RASP.
Operateur-sintaksis NORM.ST.RASP lyk so:
= NORM.ST RASP (z; integraal)
Afgeskryfde operateur NORMSDIST is so geskryf:
= NORMSTRASP (z)
Soos u kan sien, in die nuwe weergawe van die bestaande argument "Z" argument bygevoeg "Integrale". Daar moet kennis geneem word dat elke argument nodig is.
argument "Z" dui die numeriese waarde aan waarvoor die verdeling gebou word.
argument "Integrale" stel 'n logiese waarde voor wat 'n idee kan hê "WAAR" ("1") of "ONWAAR" ("0"). In die eerste geval word die integrale verspreidingsfunksie teruggestuur na die aangeduide sel, en in die tweede geval die geweegde verspreidingsfunksie.
Probleemoplossing
Om die vereiste berekening vir 'n veranderlike uit te voer, word die volgende formule toegepas:
= NORM.ST. RASP (z; integraal (1)) - 0,5
Kom ons kyk na 'n spesifieke voorbeeld met behulp van die operateur NORM.ST.RASP om 'n spesifieke probleem op te los.
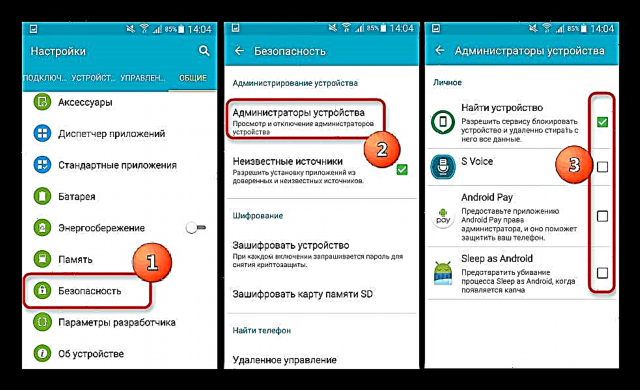
- Kies die sel waar die voltooide resultaat vertoon sal word en klik op die ikoon "Voeg funksie in"geleë naby die lyn van formules.
- Na die opening Funksie towenaars gaan na die kategorie "Statistiek" of "Volledige alfabetiese lys". Kies die naam "NORM.ST.RASP" en klik op die knoppie "OK".
- Die operateur-argumentvenster is geaktiveer NORM.ST.RASP. In die veld "Z" stel ons die veranderlike voor waarop u wil bereken. Hierdie argument kan ook voorgestel word as 'n verwysing na die sel wat hierdie veranderlike bevat. In die veld "Integrale"voer die waarde in "1". Dit beteken dat die operateur na berekening die integrale verspreidingsfunksie as oplossing sal terugstuur. Nadat bogenoemde aksies voltooi is, klik op die knoppie "OK".
- Daarna is die resultaat van dataverwerking deur die operateur NORM.ST.RASP sal vertoon word in die vakkies wat in die eerste paragraaf van hierdie handleiding aangedui word.
- Maar dit is nie al nie. Ons het slegs die standaard normale integrale verdeling bereken. Om die waarde van die Laplace-funksie te bereken, moet u die getal daarvan aftrek 0,5. Kies die sel wat die uitdrukking bevat. In die formulebalk na die stelling NORM.ST.RASP voeg die waarde by: -0,5.
- Klik op die knoppie om die berekening uit te voer Tik. Die resultaat wat verkry is, is die gewenste waarde.






Soos u kan sien, is die berekening van die Laplace-funksie vir 'n spesifieke numeriese waarde in Excel nie moeilik nie. Vir hierdie doeleindes word die standaardoperateur gebruik. NORM.ST.RASP.